Хохрякова А. Д.
Введение

Умение решать сферические треугольники требуется, начиная с регионального этапа 10 класса всероссийской олимпиады школьников по астрономии. Это позволяет преобразовывать сферические координаты из одной системы в другую, находить азимуты и моменты времени точек восхода и захода светил, получать координаты Солнца в зависимости от дня года и решать многие другие задачи.
Сферический треугольник и основные формулы сферической тригонометрии
Сферическим треугольником называется фигура на поверхности сферы, образованная дугами трех больших кругов, образующих стороны сферического треугольника. Эти углы измеряются плоскими углами при вершинах треугольника между касательными к его сторонам. Разность между суммой трех углов сферического треугольника и 180◦ называется сферическим избытком и обозначается как σ , т. е.
σ = ∠A + ∠В + ∠С −180◦
Площадь сферического треугольника s равна
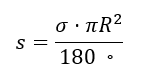
, где R — радиус сферы, на поверхности которой образован треугольник. Возьмем сферический треугольник ABC со сторонами a, b и c, образованный на сфере радиуса R с центром в точке О. Для него верны следующие соотношения:
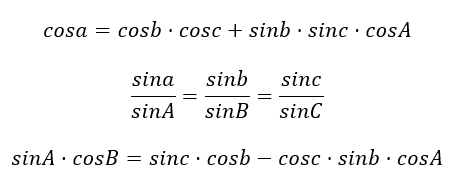
, которые называют теоремой косинусов, теоремой синусов и формулой пяти элементов соответственно.
Параллактический треугольник и преобразование координат
Параллактическим треугольником называется треугольник на небесной сфере, образованный пересечением небесного меридиана, вертикального круга и часового круга светила. Его вершинами являются полюс мира P, зенит Z и светило M.
Если светило М находится в западной половине небесной сферы, то сторона ZP (дуга небесного меридиана) равна 90◦-φ, где φ — широта места наблюдения; сторона ZM (дуга вертикального круга) равна зенитному расстоянию светила z=90◦-h, где h — высота светила, сторона PM (дуга часового круга) равна полярному расстоянию светила p=90◦-δ, где δ — склонение светила; угол ∠PZM=180◦-A, где А — азимут светила; угол ∠ZPM=t, т.е. равен часовому углу светила; угол PMZ=q называется параллактическим углом, обычно он неизвестен.
Если светило находится в восточной половине небесной сферы, то значения сторон параллактического треугольника те же, что и в случае пребывания светила в западной половине, но значения углов при вершинах Z и P иные, а именно: угол ∠PZM=A — 180◦, а угол ∠ZPM=360◦ — t.
Вид параллактического треугольника для одного и того же светила зависит от широты место наблюдения φ и от момента наблюдения, т.е. от часового угла t.
Применяя основные формулы сферической тригонометрии к параллактическому треугольнику и считая исходными сторону PM и угол t, получим
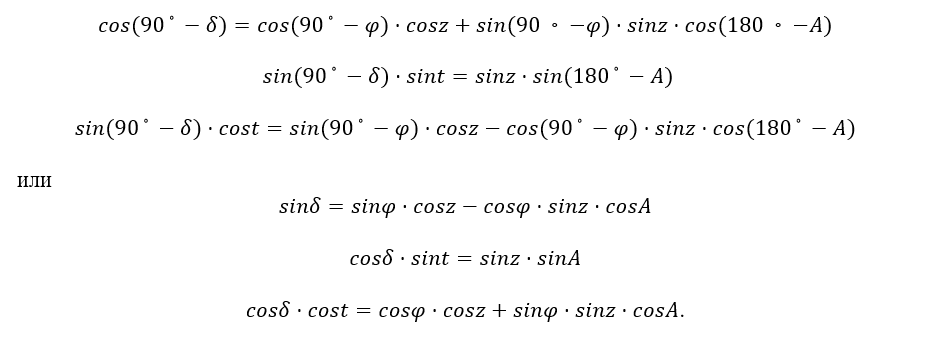
Эти формулы служат для вычисления склонения светила δ и его часового угла t (а затем и прямого восхождения α = s−t) по измеренным (или известным) его зенитному расстоянию z и азимуту A в момент звездного времени s. Иными словами, они служат для перехода от горизонтальных координат светила к его экваториальным координатам.
Аналогично можно перейти от экваториальных к горизонтальным координатам, считая исходными сторону ZM=z и угол 180◦-A:
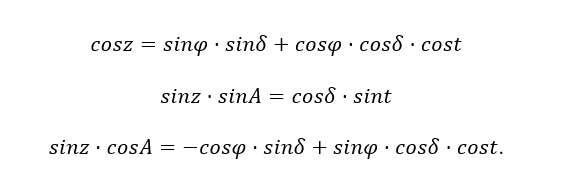
Примеры решения задач

Список литературы
[1] Кононович Э.В., Мороз В.И. Общий курс астрономии
[2] Воронцов-Вельяминов Б.А. Сборник задач и практических упражнений по астрономии
[3] Клищенко А.П., Шупляк В.И. Астрономия: Учебное пособие