Рассмотрение движения твёрдого тела является непростой задачей. Однако часто ситуация сильно упрощается за счёт использования понятия кинематических связей. В данной статье будет рассмотрено плоское движение твёрдого тела (такое движение, при котором все точки тела движутся параллельно одной плоскости). Для этого необходимо сначала напомнить, что в механике считается твёрдым телом.
Определение. Твёрдое тело — это неизменяемая система материальных точек, то есть такая идеализированная система, при любых движениях которой взаимные расстояния между материальными точками системы остаются неизменными.
Плоское движение твёрдого тела удобно тем, что, не теряя общности, можно считать само тело плоским, а движение — происходящим в плоскости тела. Из определения твёрдого тела следует, что положение плоского тела однозначно определяется заданием положения каких-либо двух его точек (для объёмного тела это не так, так как не учитывается вращение вокруг оси, проходящей через эти две точки).
Рассмотрим вращение твёрдого тела вокруг неподвижной оси. Чтобы получить представление о распределении скоростей в нём, достаточно рассмотреть движение точек тела, лежащих в какой-либо одной плоскости, перпендикулярной к оси вращения. Таким образом, мы приходим к модели плоского движения твёрдого тела. Все точки тела будут двигаться по окружностям с центром в точке O и их скорости будут пропорциональны радиусам соответствующих окружностей (см. рис. 1).
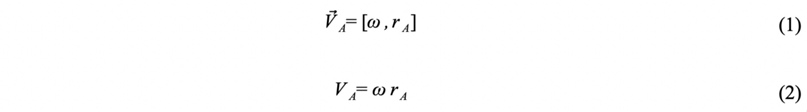
Рассмотрим теперь более общее движение плоского твёрдого тела. Плоскость вращения совпадает с плоскостью самого тела. В общем случае никакой неподвижной оси, вокруг которой происходило бы вращение тела, не предполагается.
Пусть А и B — две произвольные точки твёрдого тела. По определению твёрдого тела, расстояние между этими точками в процессе движения не меняется.
Продифференцировав это выражение, получим:
Допустим, что в рассматриваемый момент времени в теле существует точка, скорость которой в этот момент времени равна нулю. Стоит заметить, что такая точка существует для произвольного плоского движения тела. Это восходит к тому, что к твёрдому телу всегда можно мысленно добавить точку, положение которой относительно этого тела не меняется, и считать её частью твёрдого тела. Несложно убедиться, что это не идёт в противоречие с определением. Примем точку A за названную точку. Тогда формула (4) примет вид:
Это выражение будет верно для любого положения точки B. Используя понятие скалярного произведения, получаем:
Можно сделать вывод, что скорость точки B перпендикулярна к линии, соединяющей точки A и B. При движении твёрдого тела всякая прямая остаётся прямой. Это справедливо и для AB. Соответственно, поскольку в рассматриваемый момент точка А покоится, то величина скорости точки B в этот момент пропорциональна расстоянию AB (см. рис. 2). Таким образом, можно сделать вывод, что распределение скоростей в теле в рассматриваемый момент времени будет в точности таким же, как и при вращении вокруг неподвижной оси, проходящей через точку A. Движение тела в данном случае называется мгновенным вращением.
Определение. Мгновенная ось вращения — это прямая, проходящая через точки тела, скорости которых в рассматриваемый момент времени равны нулю.
Под словом «мгновенная» подразумевается, что это понятие служит для описания распределения скоростей только в какой-то заданный момент времени. В отличие от рассмотренной выше неподвижной оси, сохраняющей своё положение в теле и пространстве, мгновенная ось, вообще говоря, перемещается как в теле, так и в пространстве.
Резюмируя всё вышесказанное, можно сделать вывод, что использование мгновенной оси вращения является удобным инструментом для нахождения скоростей точек твёрдого тела в данный момент времени.
Стоит также заметить, что той же осью нельзя пользоваться для описания мгновенного распределения ускорений. Дело в том, что для определения ускорений недостаточно знать распределение скоростей только в рассматриваемый момент времени. Необходимо знать также распределение скоростей в бесконечно близкий момент времени.
Далее рассмотрим алгоритм поиска точки, принадлежащей мгновенной оси вращения. В соответствии со сказанным выше для описания движения твёрдого тела достаточно рассмотреть движение двух точек этого тела.
Случай 1. (Пусть точки не лежат на одной прямой с искомой точкой) В этом случае из каждой точки нужно построить перпендикуляры к направлениям их скоростей. Пересечение этих перпендикуляров и будет точкой, принадлежащей мгновенной оси вращения тела.
Случай 2. (Пусть точки лежат на одной прямой с искомой точкой) Если попробовать повторить алгоритм, рассмотренный в случае 1, то мы неминуемо столкнёмся с противоречием, так как сможем определить только прямую, на которой будет лежать искомая точка. На этот раз нужно провести прямую через концы векторов скоростей обеих точек. Пересечение этой прямой с линией, на которой лежат эти точки, и даст искомую точку.
Рассмотрим задачу по механике, при решении которой можно использовать понятие мгновенной оси вращения.
Задача. Пусть есть система, изображённая на рис. 3. Она состоит из стержней АВ и BC, шарнирно закреплённых друг с другом под прямым углом. Точка А также шарнирно закреплена с плоскостью опоры. Стержень АB начинает вращаться вокруг точки А с угловой скоростью ω. Длины стержней равны l. Какова будет скорость точки С?
Решение. Так как стержень АВ вращается вокруг неподвижной оси, проходящей через точку А, то скорость точки В будет сонаправлена с ВС, а модуль скорости будет вычисляться по формуле (2):
Далее рассмотрим движение точки С. Так как она не может отрываться от плоскости опоры, то её скорость направлена вдоль горизонтальной оси. Применим алгоритм нахождения мгновенного центра вращения, описанный для случая 1 выше. Иллюстрацию применения метода можно видеть на рис. 4.
Из геометрии построения видно, что
По определению мгновенной оси вращения:
Таким образом:
Ответ:
Надеюсь, после прочтения этой статьи вы стали лучше понимать кинематику твёрдого тела. Для закрепления материала рекомендую решить предложенные ниже задачи.
Задачи
Задача 1. а) Пусть диск катится по горизонтальной плоскости без проскальзывания со скоростью V. Найти мгновенную ось вращения и угловую скорость вращения относительно неё.
б) Пусть теперь диск катится по конвейеру без проскальзывания с такой же скоростью. Конвейер начинает двигаться со скоростью диска в направлении его движения. Вопрос тот же.
Задача 2. (Савченко О. Я. Сборник «Задачи по физике». № 1.5.7)
а) Скорость точки А твердого тела равна v и образует угол 45° с направлением прямой АВ. Скорость точки В этого тела равна u. Определите проекцию скорости точки В на направление АВ.
б) Скорости точек А и В твердого тела равны v. Скорость точки С, находящейся в плоскости прямой АВ и вектора v, равна u > v. Найдите проекцию скорости точки С на ось, перпендикулярную указанной плоскости.
Ответы
- а) В точке касания с горизонтальной осью. V/R, где R — радиус диска.
- б) На радиус ниже точки касания. Угловая скорость та же.
2. а) UAB = U/√2.
2. б) U₁ = √(u² – v²).
Список использованной литературы
- Сивухин Д. В. Курс общей физики. Том 1. М., 2000.
- Савченко О. Я. Задачи по физике. Новосибирск, 2008.
Автор: Артём Васюков