Гасымов Дамир
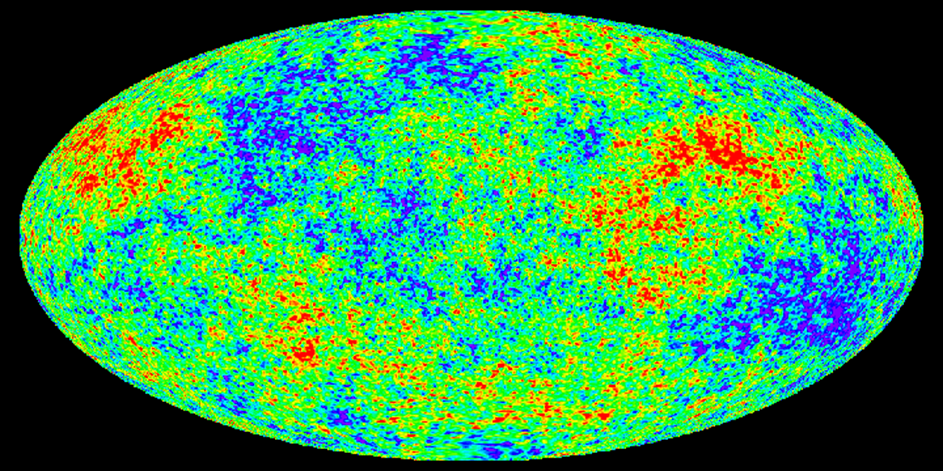
Космология, как известно, наука, изучающая свойства и эволюцию Вселенной в целом, как единого тела. Рассмотрим математическое описание простого случая, т.н. плоской Вселенной, без тёмной материи и энергии. Сумма углов треугольника в такой Вселенной равна 180 градусам.
Наша Вселенная расширяется и это было доказано Э. Хабблом в начале 20-го века. Назовём r ̃ – сопутствующей координатой, некоторым расстоянием между двумя телами в момент времени T_0 от Большого Взрыва. Также введём параметр a(t) – масштабный фактор, параметр изменения расстояния в момент времени t, т.е. R(t)=R_0*a(t). Для T_0,r ̃=R_0, а значит a(T_0)=1.
По закону Хаббла V=Hr=cz (для z много меньших 1). Значит, постоянная Хаббла равна:
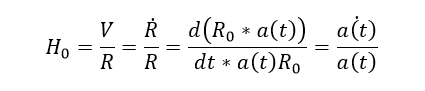
Получается, что постоянная Хаббла (один из главных параметров Вселенной) зависит от изменения масштабного фактора. Как известно по закону Доплера и определению красного смещения (длины волн можно рассматривать как сопутствующие координаты):
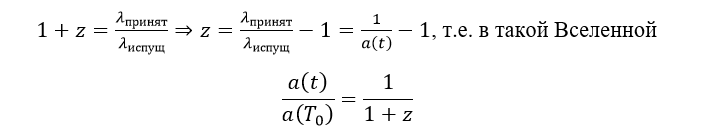
Это одно из самых важных выражений в космологии. Если подставить это выражение в формулу Планка можно получить зависимость наблюдаемой температуры объекта (например, реликтового фона) от красного смещения:
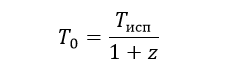
Теперь рассмотрим Вселенную как единый шар с равномерно распределённой плотностью. Для какой-то частички массой m на краю такого шара полная энергия равна 0:
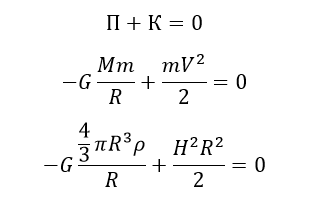
И если всё правильно сократить, мы получим формулу «критической» плотности — плотности плоской Вселенной. Если плотность Вселенной меньше «критической», то в итоге Вселенная начнёт бесконтрольно расширяться. В обратной ситуации, если плотность больше «критической», то такая Вселенная в конечном итоге сожмётся в точку:
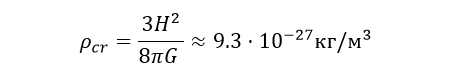
Современное значение плотности нашей Вселенной, полученное WMAP, отличается всего на 1% от полученной критической плотности, что находится в пределах погрешности измерений. Но, как известно, для замкнутой массы при увеличении радиуса Вселенной плотность будет уменьшаться. На самом деле,
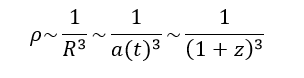
Если же вспомнить, что у нас есть тёмная энергия — вещество, плотность которого неизменно, то мы получим:
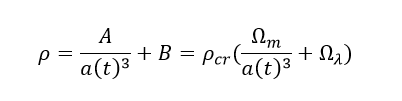

Если плотность Вселенной равна критической, то Ωm+Ωλ=1, но часто «лямбда»-членом пренебрегают и приравнивают к 0.
Из формулы понятно, что критическую плотность можно представить как: ρ=CH2, где C – некоторая константа. Значит,
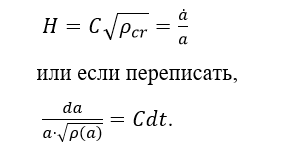
Получается, если мы будем знать зависимость критической плотности от масштабного фактора, то мы сможем получить время жизни, просуммировав функцию от 0 до T0.
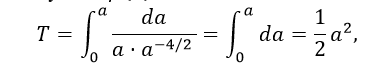
1) Рассмотрим плоскую Вселенную, для которой уже получена зависимость от масштабного фактора:
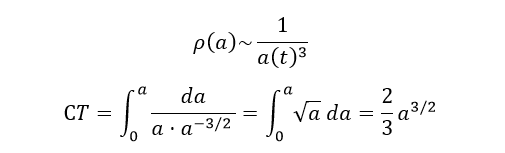
Степенной интеграл можно подсмотреть в таблице, отсюда вытекает важный для космологии плоской Вселенной факт: a~T(2/3)
2) Рассмотрим другую ситуацию, Вселенную из тёмной энергии, плотность которой постоянна, ρ(a)=const:
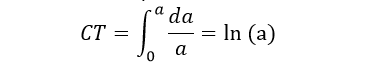
Или же a~e(CT\Righ HT).
3) И также третья ситуация ρ(a)~a-4:
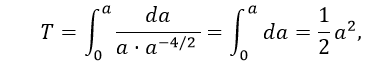
Что равносильно a~√t.
Вспомним полученное ранее выражение для постоянной Хаббла от масштабного фактора:
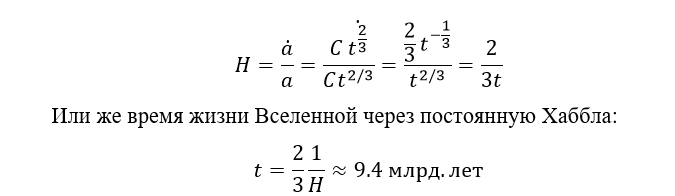
По какой причине полученное время меньше возраста самых старых звёзд? Из-за того, что мы взяли для расчёта зависимость плотности Вселенной от масштабного фактора, пренебрегая темной энергией, которая составляет около 75% массы нашей Вселенной. Кроме того, можно заметить, что величина, обратная постоянной Хаббла, с большой точностью похожа на возраст нашей Вселенной. Это не более, чем совпадение.
По материалам лекций Желтоухова С.Г.
