Преподаватели АПО помогут не только изучить самые важные темы, но и отработать форматы олимпиадных заданий на практике! Выберите подходящий вам формат занятий на странице кафедры астрономии АПО
Кирилл Львов
МГУ им. М.В. Ломоносова, физический факультет


Многие задачи астрономии, связанные с видимыми положениями и движениями небесных тел, сводятся к решению сферических треугольников. К таким задачам относятся преобразование координат из одной системы небесных координат в другую, расчёт долготы центрального меридиана планеты Солнечной системы, разметка солнечных часов и точное направление спутниковой антенны («тарелки») на нужный спутник для приёма каналов спутникового телевидения.
Мы обсудим, как рассчитывать моменты времени и азимуты восхода и захода светил в любой день года.
Сферический треугольник и формулы сферической тригонометрии.
Напомним три основных соотношения сферической тригонометрии (рис. 1)
- теорема косинусов:
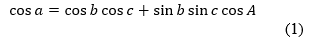
косинус стороны равен произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними.
2. формула пяти элементов:
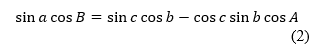
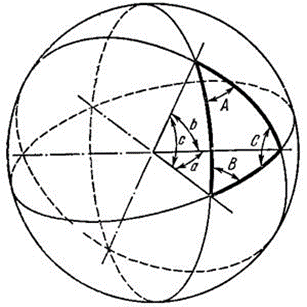
произведение синуса стороны на косинус прилежащего угла равняется произведению синуса другой стороны, ограничивающей прилежащий угол, на косинус третьей стороны минус произведение косинуса стороны, ограничивающей прилежащий угол, на синус третьей стороны и на косинус угла, противолежащего первой стороне
3. теорема синусов:

отношение синуса стороны сферического треугольника к синусу противолежащего угла есть величина постоянная.
Параллактический треугольник и преобразование координат
Как известно, в сферической астрономии для описания положения тела на небесной сфере используется несколько систем небесных координат:
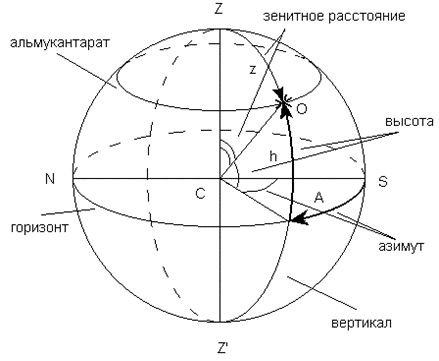
- Горизонтальная система. Положение тела задается высотой h и азимутом A. Система используется для определения направления на светило относительно земных предметов или с помощью угломерных инструментов, когда телескоп смонтирован на азимутальной установке.
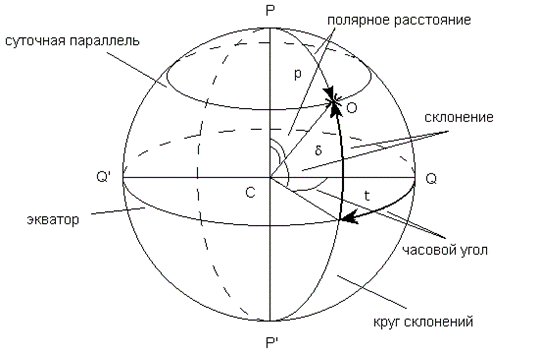
- Первая экваториальная система. Положение тела задается склонением и часовым углом t. Система используется преимущественно при определении точного времени – одной из основных задач практической астрономии, при наблюдениях на телескопе, смонтированном на экваториальной установке.
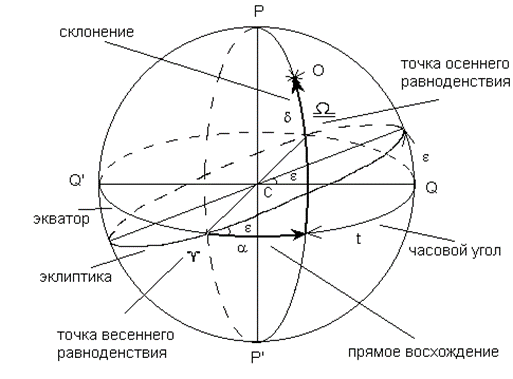
- Вторая экваториальная система. Положение тела задается склонением и прямым восхождением . Система является общепринятой в астрометрии. В этой системе составляются каталоги положений звезд и других светил, а также звездные карты.
Поэтому важно уметь переходить от одних координат светила к другим. Для этой задачи нам понадобятся формулы сферической тригонометрии.
Параллактическим треугольником называется треугольник на небесной сфере, образованный пересечением небесного меридиана, вертикального круга и часового круга светила. Его вершинами являются полюс мира Р, зенит Z и светило М. Если светило М находится в западной половине небесной сферы (рис. 5), то сторона ZP (дуга небесного меридиана) равна , где — широта места наблюдения, сторона ZM (дуга вертикального круга) равна зенитному расстоянию светила , сторона
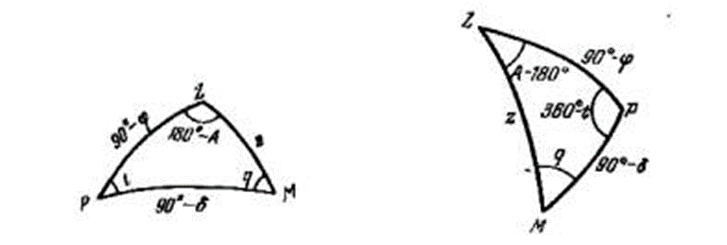
РМ (дуга часового круга) равна полярному расстоянию светила p=90°- δ; угол PZM=180°- A, угол ZPM=t, т.е. часовому углу светила, угол PMZ = q называется параллактическим углом.
Если светило находится в восточной половине небесной сферы (рис. 6), то значения сторон параллактического треугольника те же, что и в случае пребывания светила в западной половине, но значения углов при вершинах Z и Р иные, а именно: угол PZM=180°- A, а ZPM=360°- t.
Вид параллактического треугольника для одного и того же светила зависит от широты места наблюдения и от момента наблюдения, т.е. от часового угла t.
Применяя формулы (1), (2), (3) сферической тригонометрии к параллактическому треугольнику (рис. 5) и считая исходными сторону РМ и угол t, получим:
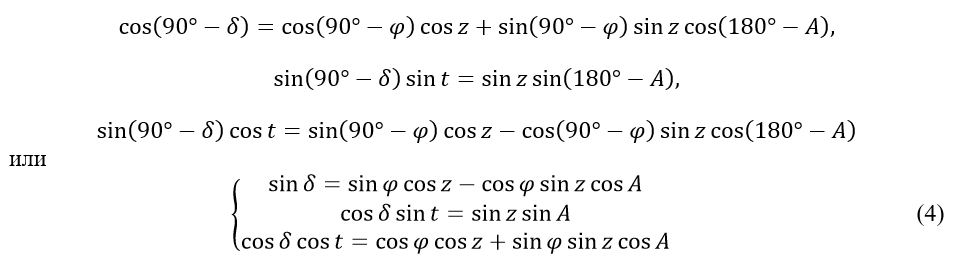
Формулы (4) служат для вычисления склонения светила и его часового угла t (а затем и прямого восхождения α=s-t) по известным его зенитному расстоянию z и азимуту A в момент звездного времени s. Звездное время для любой широты и местного времени можно найти в астрономическом справочнике (например, http://allcalc.ru/node/254). Иными словами, формулы (4) служат для перехода от горизонтальных координат светила к его экваториальным координатам.
Если исходными считать сторону ZM = z и угол PZM=180°-A, то основные формулы в применении к параллактическому треугольнику напишутся в следующем виде:
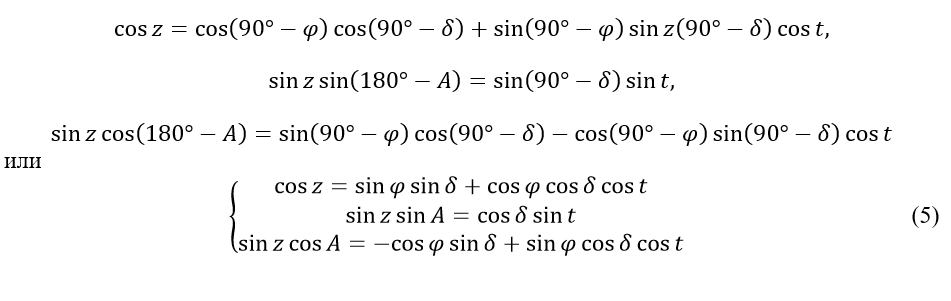
Формулы (5) служат для вычисления зенитного расстояния z и азимута светила A (для любого момента звездного времени s и для любой широты ) по известному склонению светила и его часовому углу t=s-α. Иными словами, они служат для перехода от экваториальных координат светила к его горизонтальным координатам.
Кроме того, формулы (4) и (5) используются при вычислении моментов времени восхода и захода светил и их азимутов в эти моменты, а также при решении двух очень важных задач практической астрономии — определения географической широты места наблюдения и определения местного звездного времени s.
Вычисление моментов времени и азимутов восхода и захода светил
Для вычисления моментов времени восхода и захода сначала надо вычислить часовые углы светил в это момент. Часовой угол светила определяется из первой формулы (5), а именно:
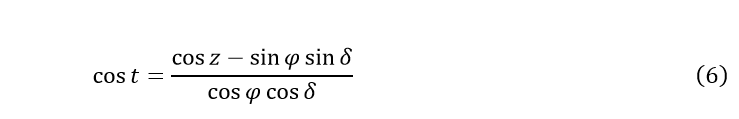
Если какая-нибудь точка небесного свода восходит или заходит, то она находится на горизонте и, следовательно, ее видимое зенитное расстояние z^’=90°. Ее истинное зенитное расстояние z в этот момент вследствие рефракции будет больше видимого на величину = 35′. Суточный параллакс понижает светило над горизонтом, т. е. увеличивает видимое зенитное расстояние z’ на величину горизонтального параллакса p= R⨁/a, где R⨁ – радиус Земли, а – расстояние от Земли до светила.
Кроме того, для Солнца и Луны, имеющих заметные размеры, координаты относятся к центру их видимого диска, а восходом (или заходом) этих светил считается момент появления (пли исчезновения) на горизонте верхней точки края диска. Следовательно, истинное зенитное расстояние центра диска этих светил в момент восхода или захода будет больше зенитного расстояния верхней точки края диска на величину видимого углового радиуса R диска. У Солнца и Луны их видимые угловые радиусы приблизительно одинаковы и в среднем равны 16′.
Следовательно, истинное зенитное расстояние точки в момент ее восхода или захода равно:
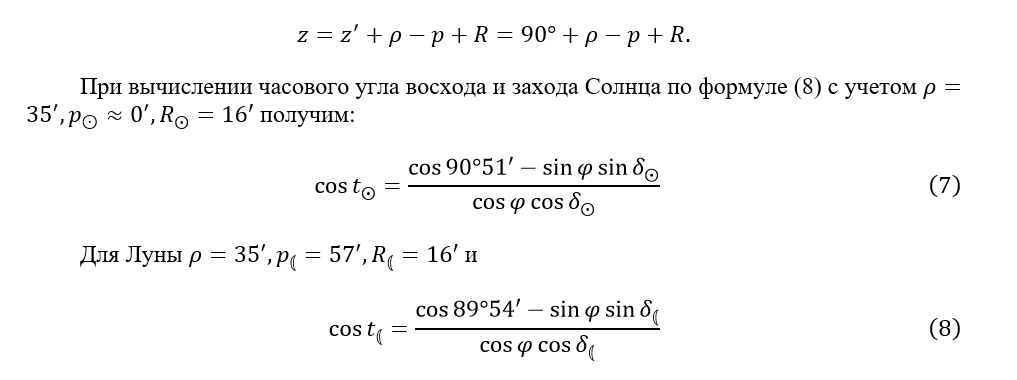
Для звезд и планет можно пренебречь также и их видимыми радиусами и вычислять часовые углы восхода и захода по формуле:
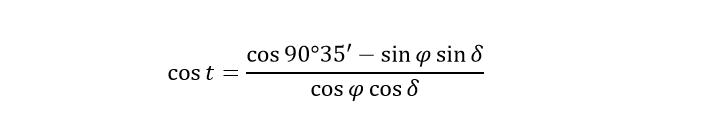
Наконец, если пренебречь и рефракцией, то часовой угол восхода и захода вычисляется по формуле:

Каждое из приведенных уравнений дает два значения часового угла. Положительное значение соответствует заходу, отрицательное — восходу светила. Местное звездное время восхода и захода получается таким:
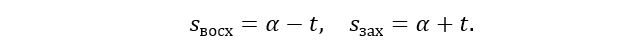
Затем можно вычислить моменты восхода и захода светила по местному среднему солнечному времени Tm или по поясному времени Tn=T0+nh (номер пояса выражен в часовой мере).
Если вычисляется восход и заход Солнца, то нет необходимости вычислять звездное время явлений, так как местное истинное солнечное время равно часовому углу Солнца, увеличенному на 12 часов. Тогда местное среднее время равно:
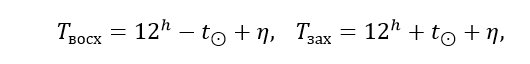
где η – уравнение времени, которое берется, также как и прямое восхождение и склонение Солнца, из Астрономического Ежегодника.
Азимуты точек восхода и захода светил (без учета рефракции, параллакса и углового радиуса) получим, если в первой формуле (4) положим z=90°, тогда sin z=1,cos z=0 и
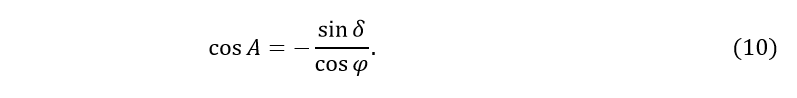
По формуле (10) получаем два значения азимута: Азах = A и Aвосх = 360° – A. Первое значение является азимутом точки захода, второе — азимутом точки восхода светила.
Наконец, представим формулы (9) и (10) в виде:
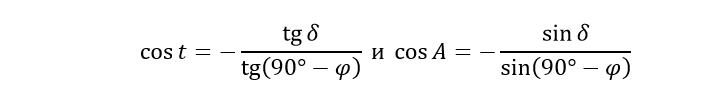
Так как косинус не может быть больше 1, то из этих формул следует, что восход и заход светила возможны только при условии:
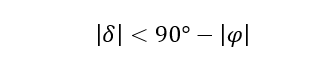
Преподаватели АПО помогут не только изучить самые важные темы, но и отработать форматы олимпиадных заданий на практике! Выберите подходящий вам формат занятий на странице кафедры астрономии АПО